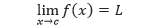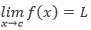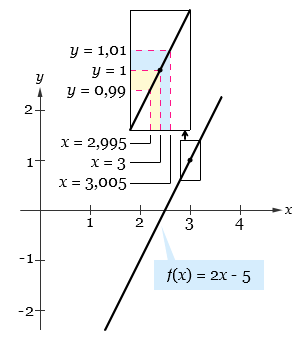Mari kita tinjau sisi lain dari definisi informal limit. Jika f(x) mendekati suatu nilai Lketika x mendekati c dari kiri ataupun kanan, maka limit f(x) dengan x mendekati c adalahL, atau dapat dituliskan
Sekilas, definisi tersebut terlihat masih menerawang. Definisi informal tersebut tidak menjelaskan arti sebenarnya dari 2 frasa: “f(x) mendekati suatu nilai L” dan “x mendekati c.”
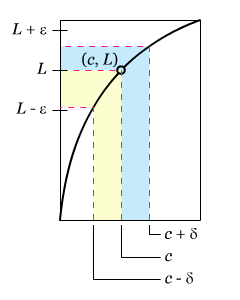
Orang pertama yang mendefiniskan limit secara matematis adalah Augustin-Louis Cauchy. Definisi limit ε-δ-nya telah digunakan sebagai standard sampai sekarang. Perhatikan gambar di bawah ini!
Pada gambar di atas, misalkan ε (epsilon) merepresentasikan bilangan positif yang kecil, maka frasa, “f(x) mendekati suatu nilai L” berarti bahwa f(x) terletak di antara interval (L– ε, L + ε). Dengan menggunakan nilai mutlak, kita dapat menuliskan pernyataan tersebut sebagai |f(x) – L| < ε.
Dengan cara yang sama, frasa “x mendekati c” berarti bahwa ada bilangan positif δ sedemikian sehingga x terletak dalam interval (c – δ, c) atau interval (c, c + δ). Pernyataan ini secara singkat dapat ditulis menjadi 2 pertidaksamaan, 0 < |x – c| < δ. Pertidaksamaan yang pertama, 0 < |x – c| (dibaca: jarak antara x dan c lebih besar dari 0), menyatakan bahwa x ≠ c. Pertidaksamaan yang kedua, |x – c| < δ, menyatakan bahwa x berjarak kurang dari δ satuan dari c.
Definisi LimitMisalkan f adalah fungsi yang terdefinisi pada selang buka yang memuat c (kemungkinan bisa hanya di kanan-kiri c) dan misalkan L adalah sebarang bilangan real. Pernyataan,
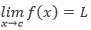
berarti bahwa untuk setiap ε > 0 ada δ > 0 sedemikian sehingga jika 0 < |x – c| < δ, maka |f(x) – L| < ε.
Beberapa fungsi tidak memiliki limit ketika x mendekati c. Akan tetapi jika suatu fungsi memiliki nilai limit, maka fungsi tersebut tidak dapat memiliki 2 nilai limit yang berbeda. Dengan kata lain, jika limit suatu fungsi ada, maka nilai tersebut haruslah unik.
Contoh-contoh berikut ini akan membantu kita untuk mengembangkan pemahaman kita mengenai definisi limit ε-δ.
Contoh 1: Menemukan δ Jika Diberikan ε
Diberikan bahwa nilai limit 2x – 5 ketika x mendekati 3 adalah 1. Tentukan δ sedemikian sehingga |(2x – 5) – 1| < 0,01 ketika 0 < |x – 3| < δ.
Pembahasan
Pada permasalah ini kita diberikan nilai ε, yaitu ε = 0,01. Untuk menentukan nilai δ, perhatikan bahwa |(2x – 5) – 1| = |2x – 6| = 2|x – 3|. Karena pertidaksamaan |(2x – 5) – 1| < 0,01 setara dengan 2|x – 3| < 0,01, maka kita dapat memilih δ = 1/2 ∙ 0,01 = 0,005. Mengapa kita harus memilih nilai δ yang demikian?
Perhatikan bahwa 0 < |x – 3| < 0,005 menyebabkan |(2x – 5) – 1| = 2|x – 3| < 2(0,005) = 0,01, seperti yang ditunjukkan oleh gambar berikut.
Pada contoh 1, yang kita lakukan adalah menentukan nilai δ jika diberikan ε. Yang kita lakukan itu tidak membuktikan keberadaan limit. Untuk membuktikannya, kita harus dapat menentukan nilai δ untuk sembarang ε, seperti yang ditunjukkan oleh contoh selanjutnya.
Contoh 2: Menggunakan Definisi Limit ε-δ
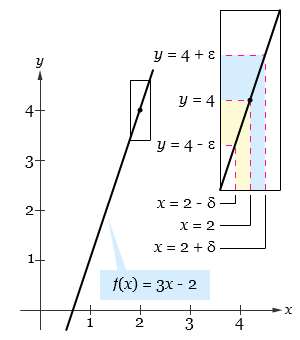
Gunakan definisi ε-δ untuk membuktikan bahwa limit 3x – 2 untuk x mendekati 2 adalah 4.
Pembahasan
Kita harus dapat menunjukkan bahwa untuk setiap ε > 0, ada δ > 0 sedemikian sehingga |(3x – 2) – 4| < ε ketika 0 < |x – 2| < δ. Karena δ nantinya bergantung pada ε, kita harus menentukan hubungan antara nilai mutlak |(3x – 2) – 4| dengan |x – 2|.
|(3x – 2) – 4| = |3x – 6| = 3|x – 2|
Sehingga, jika diberikan ε > 0 kita dapat memilih δ = ε/3. Pilihan kita ini tepat karena, 0 < |x – 2| < δ = ε/3 akan menyebabkan |(3x – 2) – 4| = 3|x – 2| < 3 ∙ ε/3 = ε, seperti yang ditunjukkan oleh gambar berikut.
Contoh 3: Menggunakan Definisi Limit ε-δ
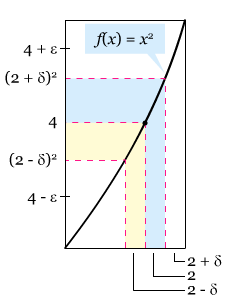
Gunakan definisi ε-δ untuk membuktikan bahwa limit x2 untuk x mendekati 2 adalah 4.
Pembahasan
Kita harus menunjukkan bahwa untuk setiap ε > 0, ada δ > 0 sedemikian sehingga |x2 – 4| < ε ketika 0 < |x – 2| < δ.
Untuk menentukan δ yang memenuhi, pertama-tama kita tulis |x2 – 4| = |x – 2||x + 2|. Untuk setiap x dalam (1, 3), x + 2 < 5 sehingga |x + 2| < 5. Jadi, kita pilih δ sebagai nilai minimum antara ε/5 dan 1, sehingga ketika 0 < |x – 2| < δ, kita memperoleh |x2 – 4| = |x– 2||x + 2| < (ε/5) ∙ 5 = ε, seperti yang ditunjukkan oleh gambar berikut.
Dari contoh-contoh di atas kita menggunakan definisi limit ε-δ untuk membuktikan nilai limit tertentu dan untuk menentukan ada tidaknya nilai limit. Untuk menentukan nilai limit, akan digunakan suatu teknik yang lebih mudah daripada menggunakan definisi limit ε-δ. Semoga bermanfaat, yos3prens.